mua-uniandes.github.io
Graphs
Overview
Graphs are one of the most important mathematical concepts in Computer Science. They allow the study of interrelations between units that interact with others. As for their applications, they are found in Artficial Intelligence, Data Mining, Game Development, GeoInformatics, and a host of other disciplines.
Concepts
A Graph consists of nodes (also known as vertices) that are connected through edges. As for the purpose of these notes, the variable V will denote the number of nodes in a graph, and the variable E will denote the number of edges.

A Path leads from a node to another node through the edges of the graph. The length of a path is the number of edges in it.

A cycle is a path where the first and last node is the same. A graph is connected if there is a path between any two nodes. The connected parts of a graph are called its components. A tree is a connected graph that does not contain cycles. In a directed graph, the edges can be traversed in one direction only.
In a weighted graph, each edge is assigned a weight. The weights are often interpreted as edge lengths, and the length of a path is the sum of its edge weights. Two nodes are neighbors or adjacent if there is an edge between them. The degree of a node is the number of its neighbors. The sum of degrees in a graph is always 2E, because each edge increases the degree of exactly two nodes by one. For this reason, the sum of degrees is always even. A graph is regular if the degree of every node is a constant d. A graph is complete if the degree of every node is n −1, i.e., the graph contains all possible edges between the nodes.
In a directed graph, the indegree of a node is the number of edges that end at the node, and the outdegree of a node is the number of edges that start at the node.
A graph is bipartite if it is possible to color its nodes using two colors in such a way that no adjacent nodes have the same color. It turns out that a graph is bipartite exactly when it does not have a cycle with an odd number of edges.
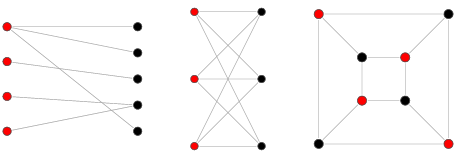
Graph Representations
id| Representation| ——–|——————- GR18-AL| Adjacency List GR18-AM| Adjacency Matrix GR18-EL| Edge List
Algorithms
id| Type|Name ——–|——————-|—————– GA18-DFS| Search | Depth-First Search GA18-BFS| Search | Breadth-First Search GA18-DJK| Shortest Path |Dijkstra GA18-BFD| Shortest Path |Bellman-Ford GA18-FWL| Shortest Path |Floyd-Warshall
Problem sets
Easy
Problem| Description| Java solution | C++ solution | Python solution | KT solution ——–|—————-|—————–|————–|————–|————– Monk at the graph factory| Determine if the graph is a tree| Java Solution| C++ Solution Learning graph| Identify graph properties| Java Solution
Medium
Problem| Description| Java solution | C++ solution | Python solution | KT solution ——–|—————-|—————–|————–|————–|————– Example| Example| Example
Hard
Problem| Description| Java solution | C++ solution | Python solution | KT solution ——–|—————-|—————–|————–|————–|————– Example| Example| Example